演算法作業 week 8

第一題

  • 題目 demo

  • tree search demo

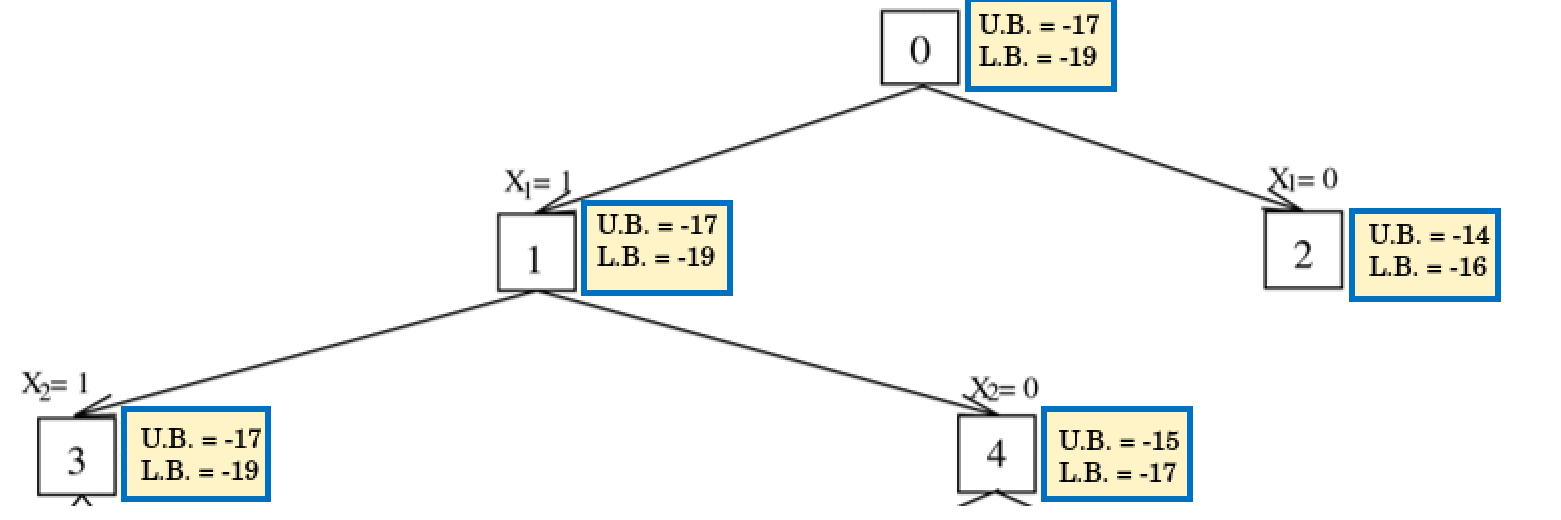
0: U.B. = -(7 + 10) = -17, L.B. = -(7 + 10 + 4 * (5 / 8)) => -19
1: U.B. = -(7 + 10) = -17, L.B. = -(7 + 10 + 4 * (5 / 8)) => -19
2: U.B. = -(10 + 4) = -14, L.B. = -(10 + 4 + 4 * (7 / 10)) => -16
3: U.B. = -(7 + 10) = -17, L.B. = -(7 + 10 + 4 * (5 / 8)) => -19
4: U.B. = -(7 + 4 + 4) = -15, L.B. = -(7 + 4 + 4 + 4 * (6 / 12)) => -17

第二題

  • 題目 demo

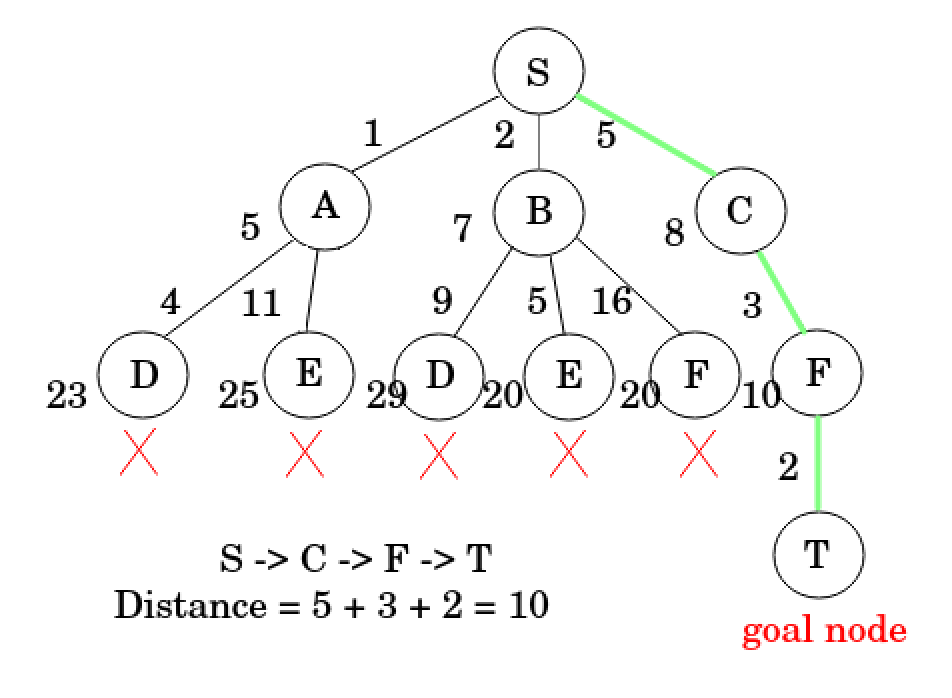
  • select S

g(A) = 1, h(A) = min(4, 11) = 4, f(A) = 1 + 4 = 5
g(B) = 2, h(B) = min(9, 5, 16) = 5, f(B) = 2 + 5 = 7
g(C) = 5, h(C) = min(3) = 3, f(C) = 5 + 3 = 8

  • select A

g(D) = 1 + 4 = 5, h(D) = min(18) = 18, f(D) = 5 + 18 = 23
g(E) = 1 + 11 = 12, h(E) = min(13) = 13, f(E) = 12 + 13 = 25

  • select B

g(D) = 2 + 9 = 11, h(D) = min(18) = 18, f(D) = 11 + 18 = 29
g(E) = 2 + 5 = 7, h(E) = min(13) = 13, f(E) = 7 + 13 = 20
g(F) = 2 + 16 = 18, h(F) = min(2) = 2, f(F) = 18 + 2 = 20

  • select C

g(F) = 5 + 3 = 8, h(F) = min(2) = 2, f(F) = 8 + 2 = 10

  • select F

g(T) = 8 + 2 = 10 （T is selected, terminate）

  • T is goal node demo

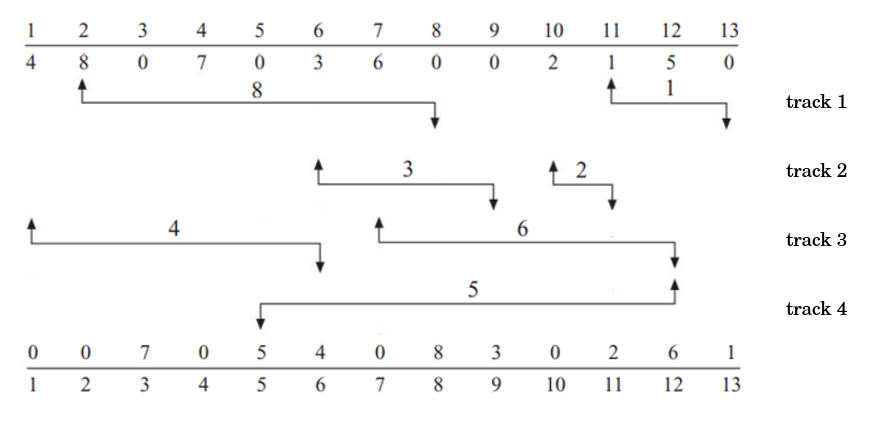
第三題

  • 題目 demo

  • horizontal demo

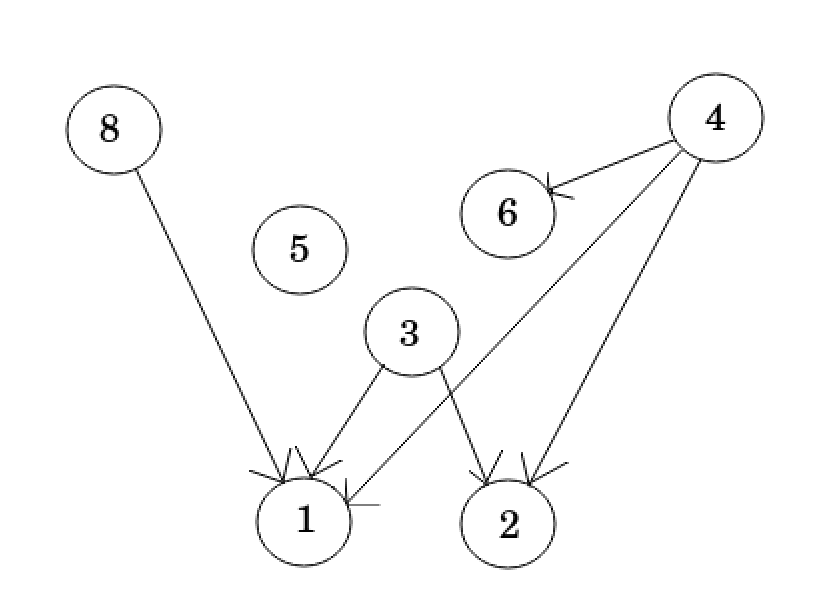
  • vertical demo

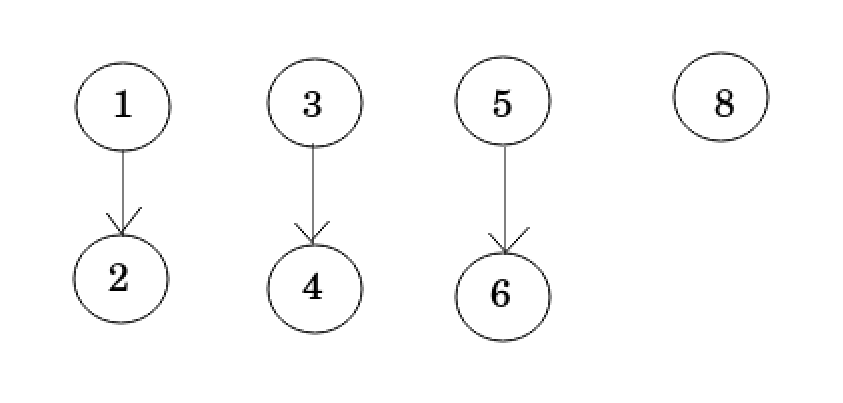
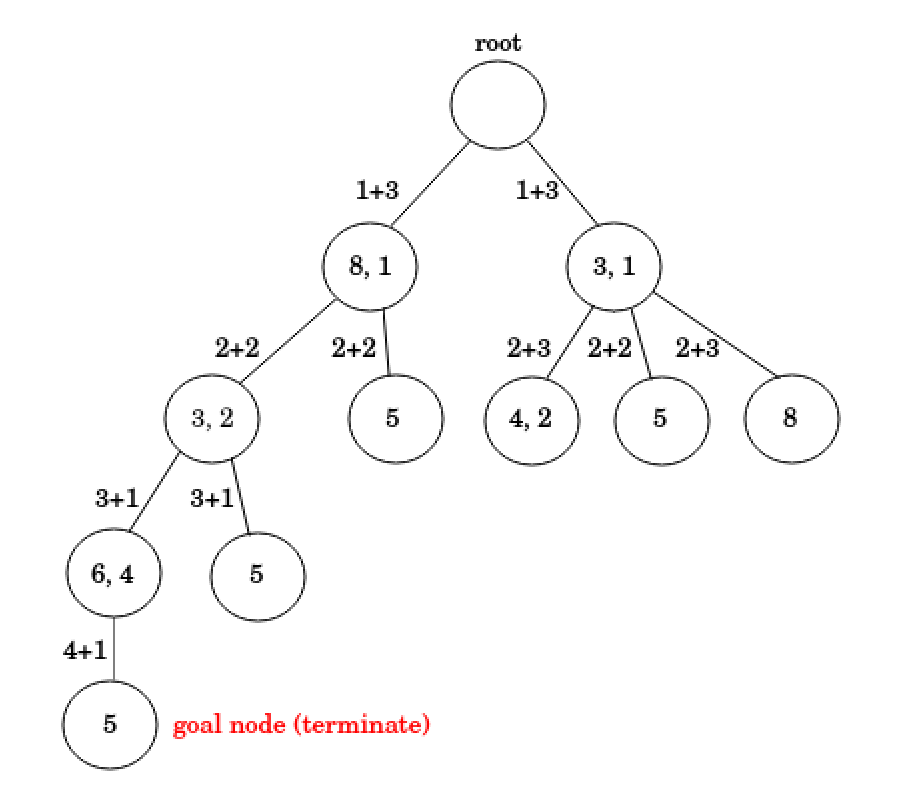
  • Maximum cliques

    {8, 1}, {3, 1}

  • local density（A* algorithm）

    • select root

    {8, 1}: 1, 2, 3, 3, 3, 3, 3, 3, 2, max = 3
    {3, 1}: 1, 2, 3, 3, 3, 3, 3, 3, 2, max = 3

    • select {8,1} first

    {3, 2}: 1, 2, 2, 2, 2, max = 2 {5}: 1, 2, 2, 2, 2, 2, 1, max = 2

    • and select {3, 1}

    {4, 2}: 1, 2, 3, 3, 3, 3, 2, max = 3 {5}： 1, 2, 2, 2, 2, 2, 1, max = 2 {8}: 1, 2, 2, 3, 3, 2, max = 3

    • select {3, 2}

    {6, 4}: 1, 1, max = 1 {5}: 1, 1, 1, 1, max = 1

    • select {6, 4} （快放完）

    {5}: 1, max = 1

  • A* algorithm（best first search） demo

  • result demo

第四題

  • BFS
class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        def exist(node):
            return node is not None

        if exist(root1) == False:
            return root2

        if exist(root2) == False:
            return root1

        queue = [root1, root2]
        while queue:
            first = queue.pop(0)
            second = queue.pop(0)

            if exist(first) and exist(second):
                first.val += second.val

            if exist(second.left):
                if exist(first.left) == False:
                    first.left = second.left
                else:
                    queue.append(first.left)
                    queue.append(second.left)
            if exist(second.right):
                if exist(first.right) == False:
                    first.right = second.right
                else:
                    queue.append(first.right)
                    queue.append(second.right)

        return root1
  • DFS
class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        def exist(node):
            return node is not None

        if exist(root1) == False and exist(root2) == False:
            return None
        elif exist(root1) == False:
            root = root2
            root.left = self.mergeTrees(None, root2.left)
            root.right = self.mergeTrees(None, root2.right)
        elif exist(root2) == False:
            root = root1
            root.left = self.mergeTrees(root1.left, None)
            root.right = self.mergeTrees(root1.right, None)
        else:
            root = TreeNode(root1.val + root2.val)
            root.left = self.mergeTrees(root1.left, root2.left)
            root.right = self.mergeTrees(root1.right, root2.right)

        return root
  • 題目連結：617. Merge Two Binary Trees - LeetCode
  • LeetCode 執行結果： demo
  • 語言：Python
  • 花費時間：一小時（BFS）、20 分鐘（DFS）
  • 完成程度：參考別人
  • 其他：root1 當基底，把 root2 的該節點加入到 root1，若是 root1 該節點不存在，則替代成 root2 的節點； 若是 root2 該節點不存在，root1 該節點就不採取動作；若兩個 root 該節點都不存在，則節點為 None。 而遍歷的方式則採用 queue 這個資料結構來協助。

第五題

class Solution:
    def lcaDeepestLeaves(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def calLCA(root, a, b):
            if root is None:
                return None

            if root.val == a.val or root.val == b.val:
                return root

            left = calLCA(root.left, a, b)
            right = calLCA(root.right, a, b)

            if left and right:
                return root
            elif left:
                return left
            elif right:
                return right

        left_most = None
        right_most = None
        queue = [root]
        while queue:
            length = len(queue)
            for i in range(length):
                node = queue.pop(0)
                if i == 0:
                    left_most = node
                if i == length - 1:
                    right_most = node
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

        return calLCA(root, left_most, right_most)
  • 題目連結：1123. Lowest Common Ancestor of Deepest Leaves - LeetCode
  • LeetCode 執行結果： demo
  • 語言：Python
  • 花費時間：一小時
  • 完成程度：參考別人
  • 其他：這題是使用 BFS 遍歷，加上 DFS 計算 LCA（Lowest Common Ancestor），其中的巧思是找到 leftmost 與 rightmost 的節點帶入 calLCA() 計算共同節點是哪個。

本週心得

畫圖好累…
果然 NP-Complete 的問題解法都很沒效率 = =

至於程式 BFS iterative 的部分真的很難想，連觀摩別人的程式碼，都要花很久的時間才能理解。

參考